Enoncé
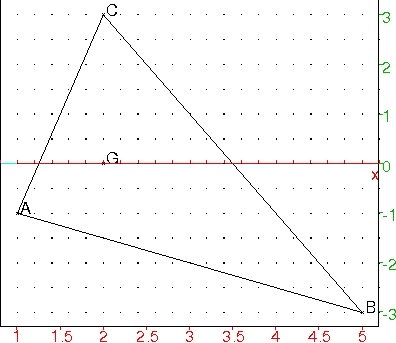
On donne $A(1~;~-1)$, $B(5~;~-3)$, $C(2~;~3)$ et $G(2~;~0)$.
Déterminer les nombres coefficients entiers $\alpha$, $\beta$ et $\gamma$ tels que $G$ soit le barycentre des points $(A,\alpha)$, $(B,\beta)$ et $(C,\gamma)$.
Résolution à l’aide de Xcas
On commence dans une session Xcas par ouvrir une fenêtre de géométrie 2D :
Menu Editer –> ajouter –> geo2d exact
A gauche de la fenêtre graphique, on rentre les instructions suivantes :
A:=point(1,-1);
B:=point(5,-3);
C:=point(2,3);
triangle(A,B,C);
G:=point(2,0);
On cherche dans un premier temps des coefficients $b$ et $c$ tels que $G$ soit le barycentre des points $(A,1)$, $(B,b)$ et $(C,c)$.
v:vecteur(G,A)+b*vecteur(G,B)+c*vecteur(G,C);
Pour visualiser les coordonnées du vecteur :
coordonnees(v)
$$[1+3b-2,-1-3b+3c]$$
On résout le système :
resoudre_systeme_lineaire([abscisse(v)=0,ordonnee(v)=0],[b,c])
$$[\dfrac13,\dfrac23]$$
En multipliant les coefficients par $3$, on retombe sur des entiers.
On vérifie en demandant les coordonnées du barycentre en question qui doivent correspondre à celles de $G$ ;
coordonnees(barycentre([A,3],[B,1],[C,2]))
$$[2,0]$$
