Un exemple
Je cherche à créer le tableau de valeurs de la fonctions $f(x)=\dfracxx+3$ pour $x$ compris entre $-2$ et $3$ avec un pas de 0.5.
Avec le tableur
On commence par créer l’expression :
f:=x/(x+3)
$$ \dfracxx+3$$
On ouvre un tableur :
Menu Editer –> Ajouter > Tableur
On configure le tableur en complétant le formulaire qui apparaît.
On peut notamment cocher l’option « graphique » si on veut que le graphe de la fonction apparaisse.
Dans la case A0, on tape :
tablefunc(f,x,-2,0.5)
Xcas calcule alors un tableau similaire à ceux créés par les calculatrices TI.
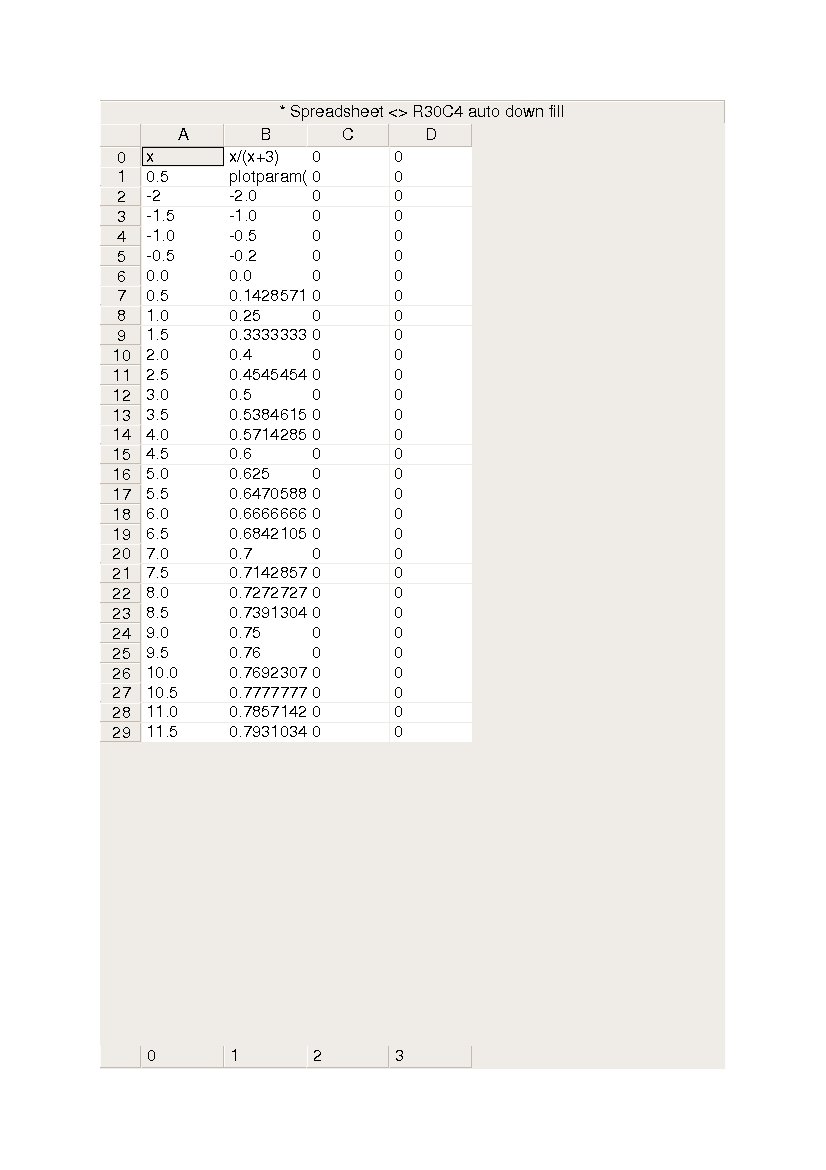
Pour changer le format des valeurs, il faut adaper les formules de la colonne B à partir de la case $B3$. On remplace :
=evalf(subst(B$0,A$0,A2))
par
=format(subst(B$0,A$0,A2),"f3")
puis on « tire » cette formule vers le bas pour la recopier.
Sans utiliser le tableur
On commence par créer la fonction :
f(x):=x/(x+3)
$$x -> \dfracxx+3$$
Pour avoir les valeurs approchées avec 3 chiffre après la virgule, on utlise le format « f3 » :
prepend(seq([x,format(f(x),"f3")],x,-2,3,0.5),[x,"f(x)"])
$$\left[\beginarraycc x & \mboxf(x) \\ -2 & \mbox-2 \\ -1.5 & \mbox-1 \\ -1.0 & \mbox-0.5 \\ -0.5 & \mbox-0.2 \\ 0.0 & 0 \\ 0.5 & \mbox0.143 \\ 1.0 & \mbox0.25 \\ 1.5 & \mbox0.333 \\ 2.0 & \mbox0.4 \\ 2.5 & \mbox0.455 \\ 3.0 & \mbox0.5 \endarray\right] $$
Si on veut le tableau horizontalement :
tran(prepend(seq([x,format(f(x),"f3")],x,-2,3,0.5),[x,"f(x)"]))
$$ \left[\beginarraycccccccccccc x & -2 & -1.5 & -1.0 & -0.5 & 0.0 & 0.5 & 1.0 & 1.5 & 2.0 & 2.5 & 3.0 \\ \mboxf(x) & \mbox-2 & \mbox-1 & \mbox-0.5 & \mbox-0.2 & 0 & \mbox0.143 & \mbox0.25 & \mbox0.333 & \mbox0.4 & \mbox0.455 & \mbox0.5 \endarray\right] $$
Si on veut les valeurs exactes, il est important de ne pas rentrer de nombres décimaux dans les paramètres : On remplacera ainsi le $0.5$ par $\dfrac12$ :
tran(prepend(seq([x,f(x))],x,-2,3,1/2),[x,"f(x)"]))
$$ \left[\beginarraycccccccccccc x & -2 & \dfrac-32 & -1 & \dfrac-12 & 0 & \dfrac12 & 1 & \dfrac32 & 2 & \dfrac52 & 3 \\ &&&&&&&&&&&\\ \mboxf(x) & -2 & -1 & \dfrac-12 & \dfrac-15 & 0 & \dfrac17 & \dfrac14 & \dfrac13 & \dfrac25 & \dfrac511 & \dfrac12 \endarray\right] $$