Enoncé
Soit la série statistique suivante :
| $X$ | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| Effectifs | 45 | 20 | 5 | 30 | 35 | 15 | 50 |
1) Donner les principaux paramètres de cette série (moyenne, écart-type, …)
2) Tracer le diagramme en bâtons correspondant.
3) Tracer le camembert correspondant.
Résolution à l’aide de Xcas
X:=[0,5,10,15,20,25,30]
$$[0,5,10,15,20,25,30]$$
Effectifs:=[45,20,5,30,35,15,50]
$$[45,20,5,30,35,15,50]$$
1) Donner les principaux paramètres de cette série (moyenne, écart-type, …)
var1stat_eff_e(X,E):=
local x,y,S;
print("- N : "+normal(sum(E))+";");
print("- Moyenne : "+normal(moyenne(X,E))+";");
print("- Variance : "+normal(variance(X,E))+";");
print("- Ecart-type : "+normal(ecart_type(X,E))+";");
S:=zip((x,y)->x*y,X,E);
print("- Somme : "+normal(sum(S))+";");
S:=zip((x,y)->x^2*y,X,E);
print("- Somme des x^2 : "+normal(sum(S))+";");
print("- Médiane : "+normal(median(X,E))+";");
print("- Q1 : "+normal(quartile1(X,E))+";");
print("- Q3 : "+normal(quartile3(X,E))+";");
print("- D1 : "+normal(quantile(X,E,0.1))+";");
print("- D9 : "+normal(quantile(X,E,0.9))+";");
print("- Min : "+normal(min(X))+";");
print("- Max : "+normal(max(X))+";");
:;
// Success
// Success
// Parsing var1stat_eff_e
// Success compiling var1stat_eff_e
var1stat_eff_e(X,Effectifs)
« – N : 200; »
« – Moyenne : 127/8; »
« – Variance : 8231/64; »
« – Ecart-type : sqrt(8231)/8; »
« – Somme : 3175; »
« – Somme des x^2 : 2275; »
« – Médiane : 20.0; »
« – Q1 : 15.0; »
« – Q3 : 25.0; »
« – D1 : 5.0; »
« – D9 : 30.0; »
« – Min : 0; »
« – Max : 30; »
Si on veut les valeurs approchées :
var1stat_eff_a(X,E):=
local x,y,S;
print("- N : "+sum(E)+";");
print("- Moyenne : "+evalf(moyenne(X,E))+";");
print("- Variance : "+evalf(variance(X,E))+";");
print("- Ecart-type : "+evalf(ecart_type(X,E))+";");
S:=zip((x,y)->x*y,X,E);
print("- Somme : "+evalf(sum(S))+";");
S:=zip((x,y)->x^2*y,X,E);
print("- Somme des x^2 : "+evalf(sum(S))+";");
print("- Médiane : "+evalf(median(X,E))+";");
print("- Q1 : "+evalf(quartile1(X,E))+";");
print("- Q3 : "+evalf(quartile3(X,E))+";");
print("- D1 : "+evalf(quantile(X,E,0.1))+";");
print("- D9 : "+evalf(quantile(X,E,0.9))+";");
print("- Min : "+evalf(min(X))+";");
print("- Max : "+evalf(max(X))+";");
:;
// Success
// Success
// Parsing var1stat_eff_a
// Success compiling var1stat_eff_a
var1stat_eff_a(X,Effectifs)
« – N : 200; »
« – Moyenne : 15.875; »
« – Variance : 128.609375; »
« – Ecart-type : 11.3406073471; »
« – Somme : 3175.0; »
« – Somme des x^2 : 2275.0; »
« – Médiane : 20.0; »
« – Q1 : 15.0; »
« – Q3 : 25.0; »
« – D1 : 5.0; »
« – D9 : 30.0; »
« – Min : 0.0; »
« – Max : 30.0; »
2) Tracer le diagramme en bâtons correspondant.
diagramme_batons(X,Effectifs)
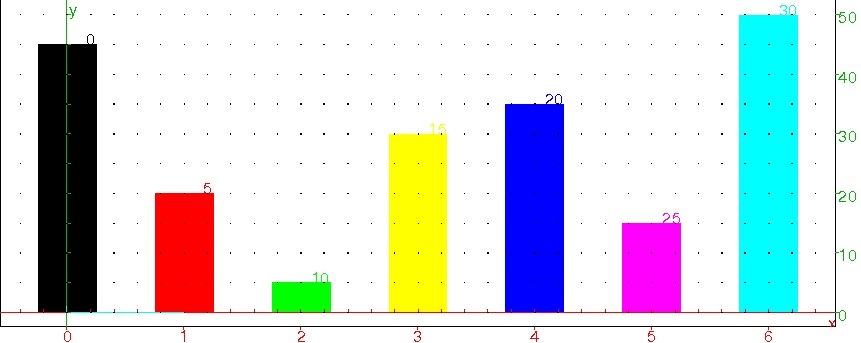
3) Tracer le camembert correspondant.
camembert(X,Effectifs)
