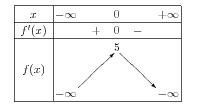
Voici son code :
\begin{center}
\begin{variations}
x &\mI& & 0 & &\pI\\
\filet
f'(x) & & + & 0 & - & \\
\filet
\m{f(x)}&\mI&\c &\h{5}&\d &\mI\\
\end{variations}
\end{center}

Voici son code :
\begin{center}
\begin{variations}
x & & 0 & & 4 & &\pI\\
\filet
f'(x) &\bg& & + & 0 & - & \\
\filet
\m{f(x)}&\bg&\mI&\c &\h{5}&\d &\mI\\
\end{variations}
\end{center}
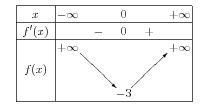
Voici son code :
\begin{center}
\begin{variations}
x &\mI & & 0 & &\pI \\
\filet
f'(x) & & - & 0 & + & \\
\filet
\m{f(x)}&\h{\pI}&\d &-3 &\c &\h{\pI}\\
\end{variations}
\end{center}
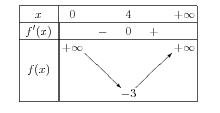
Voici son code :
\begin{center}
\begin{variations}
x & & 0 & & 4 & &\pI \\
\filet
f'(x) &\bg& & - & 0 & + & \\
\filet
\m{f(x)}&\bg&\h{\pI}&\d &-3 &\c &\h{\pI}\\
\end{variations}
\end{center}
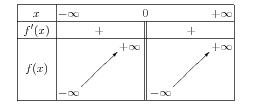
Voici son code :
\begin{center}
\begin{variations}
x &\mI& & & 0 & & &\pI \\
\filet
f'(x) & & + & &\bb& & + & \\
\filet
\m{f(x)}&\mI&\c &\h{\pI}&\bb&\mI&\c &\h{\pI}\\
\end{variations}
\end{center}

Voici son code :
\begin{center}
\begin{variations}
x &\mI& & & 0 & & &\pI\\
\filet
f'(x) & & + & &\bb& & - & \\
\filet
\m{f(x)}&\mI&\c &\h{\pI}&\bb&\h{\pI}&\d &\mI\\
\end{variations}
\end{center}

Voici son code :
\begin{center}
\begin{variations}
x &\mI & & & 0 & & &\pI \\
\filet
f'(x) & & - & &\bb& & + & \\
\filet
\m{f(x)}&\h{\pI}&\d &\mI&\bb&\mI&\c &\h{\pI}\\
\end{variations}
\end{center}
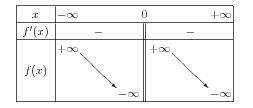
Voici son code :
\begin{center}
\begin{variations}
x &\mI & & & 0 & & &\pI\\
\filet
f'(x) & & - & &\bb& & - & \\
\filet
\m{f(x)}&\h{\pI}&\d &\mI&\bb&\h{\pI}&\d &\mI\\
\end{variations}
\end{center}