Les transformations

Rotation

image := objet rotatedaround(centre,angle);

image := rotation(objet,centre,angle);

Symétrie centrale

image := objet rotatedaround(centre,180);

image := symetrie(objet,centre);

Symétrie axiale d’axe (AB)

image := objet reflectedabout(point_A,point_B);

image := symetrie(objet,point_A,point_B);

Translation de vecteur $\overrightarrow{AB}$

image := objet shifted (point_B-point_A);

Exemples

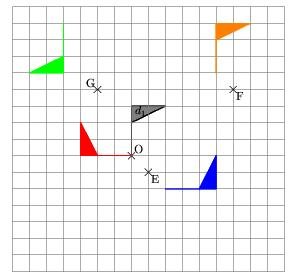
Voici une figure résumant les utilisations possibles. On y trouve des images du drapeau gris :
– par la rotation de centre O, de 90º dans le sens inverse des aiguilles d’une montre (figure rouge) ;
– par la symétrie de centre G (figure verte) ;
– par la symétrie d’axe (EF) (figure bleue) ;
– par la translation de vecteur $\overrightarrow{EF}$ (figure orange).

Voici son code dans lequel on peut noter l’utilisation du type picture :

u:=1cm;
figure (0,0,8u,8u);
pair O,E,F,G;

O=(3.5u,3.5u);
E=(4u,3u);
F=(6.5u,5.5u);
G=(2.5u,5.5u);

picture figd,figi;
currentpicture:=nullpicture;

path tri,piquet;
tri:=(3.5u,5u)--(4.5u,5u)--(3.5u,4.5u)--cycle ;
fill tri withcolor 0.5[black,white];
trace tri withpen pencircle scaled 1.5bp;
piquet:=O--(3.5u,4.5u);
trace piquet withpen pencircle scaled 1.5bp;

figd:=currentpicture;


trace grille(0.5) withcolor 0.5[black,white];

marque_p:="croix";
nomme.urt(O);
nomme.lrt(E);
nomme.lrt(F);
nomme.ulft(G);

label.rt(btex  $d_1$ etex,(3.5u,4.85u));


figi := rotation(figd,O,90);  %rotation
%figi := figd rotatedaround(O,90);
draw figi withcolor red;


figi := symetrie(figd,G);   %symetrie centrale
%figi :=figd rotatedaround(G,180);
draw figi withcolor green;


figi := symetrie(figd,E,F);   %symetrie axiale
%figi := figd reflectedabout(E,F);
draw figi withcolor blue;


figi := figd shifted (F-E);  %translation de vecteur EF
draw figi withcolor orange;


fin;