Des exemples de solides

Le cube

Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,C,D,E,F,G,H;
pair V;

numeric c;
c:=4;   %côté du cube

A=(0,0);
B=(c*u,0);
C=(c*u,c*u);
D=(0,c*u);

V=(2u,u);  % vecteur pour la perspective

E= A shifted V;
F= B shifted V;
G= C shifted V;
H= D shifted V;

draw A--B--C--D--cycle;
draw B--F--G--C;
draw G--H--D;

draw A--E--F dashed evenly;
draw H--E dashed evenly;

label.llft(btex $A$ etex,A);
label.lrt(btex $B$ etex,B);
label.lrt(btex $C$ etex,C);
label.ulft(btex $D$ etex,D);
label.lrt(btex $E$ etex,E);
label.rt(btex $F$ etex,F);
label.top(btex $G$ etex,G);
label.top(btex $H$ etex,H);


fin;

---

Le pavé droit

Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,C,D,E,F,G,H;
pair V;

numeric AB,AD;
AB:=6;  %dimensions de la face avant
AD:=3;

A=(0,0);
B=(AB*u,0);
C=(AB*u,AD*u);
D=(0,AD*u);

V=(2u,u);  % vecteur pour la perspective

E= A shifted V;
F= B shifted V;
G= C shifted V;
H= D shifted V;

draw A--B--C--D--cycle;
draw B--F--G--C;
draw G--H--D;

draw A--E--F dashed evenly;
draw H--E dashed evenly;

label.llft(btex $A$ etex,A);
label.lrt(btex $B$ etex,B);
label.lrt(btex $C$ etex,C);
label.ulft(btex $D$ etex,D);
label.lrt(btex $E$ etex,E);
label.rt(btex $F$ etex,F);
label.top(btex $G$ etex,G);
label.top(btex $H$ etex,H);

trace cotation(A,B,-5mm,2mm,btex $L$ etex);
trace cotation(A,D,5mm,2mm,btex $h$ etex rotated -90);
trace cotation(B,F,-5mm,2mm,btex $l$ etex);


fin;

---

Le tétraèdre

u:=1cm;
figure (-8u,-8u,10u,8u);
pair S,A,B,C;
A=(0,0);
B=(3u,-u);
C=(4u,u);
S=(1.5u,5u);
draw S--A;
draw S--B;
draw S--C;
draw A--C dashed evenly;
draw A--B--C;
nomme.lft(A);
nomme.bot(B);
nomme.rt(C);
nomme.top(S);
fin;

---

La pyramide

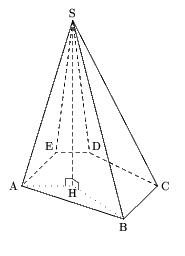
Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair S,A,B,C,D,E,H;

A=(0,0);
B=(3u,-u);
C=(4u,0);
D=(2u,u);
E=(u,u);

H=(1.5u,0);
S=(1.5u,5u);

draw S--A;
draw S--B;
draw S--C;
draw S--D dashed evenly;
draw S--E dashed evenly;

draw A--B--C;
draw C--D--E--A dashed evenly;

draw S--H dashed evenly;

draw H--A dashed withdots;
draw H--B dashed withdots;

trace codeperp(S,H,A,6);
trace codeperp(S,H,B,6);

nomme.lft(A);
nomme.bot(B);
nomme.rt(C);
nomme.urt(D);
nomme.ulft(E);
nomme.top(S);
nomme.bot(H);


fin;

---

La pyramide régulière à base carrée

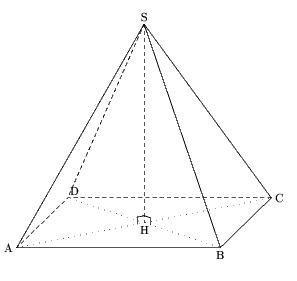
Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair S,A,B,C,D,H;
pair V;

numeric h;
h:=6;   %hauteur

A=(0,0);
B=(6u,0);

V=(1.5u,1.5u);


C=B shifted V;
D=A shifted V;


H=0.5[A,C];
S=H shifted (0,h*u);

draw S--A;
draw S--B;
draw S--C;
draw S--D dashed evenly;


draw A--B--C;
draw C--D--A dashed evenly;

draw S--H dashed evenly;

draw C--A dashed withdots;
draw D--B dashed withdots;

trace codeperp(S,H,A,6);
trace codeperp(S,H,B,6);

nomme.lft(A);
nomme.bot(B);
nomme.rt(C);
nomme.urt(D);
nomme.top(S);
nomme.bot(H);


fin;

---

la pyramide régulière à base carrée et sa réduction

Voici son code:

u:=1cm;
figure (-8u,-8u,10u,12u);
pair S,A,B,C,D,H;
pair V;

numeric h;
h:=6;   %hauteur

A=(0,0);
B=(6u,0);

V=(1.5u,1.5u);


C=B shifted V;
D=A shifted V;


H=0.5[A,C];
S=H shifted (0,h*u);

draw S--A;
draw S--B;
draw S--C;
draw S--D dashed evenly;

draw A--B--C;
draw C--D--A dashed evenly;
draw S--H dashed evenly;
draw C--A dashed withdots;
draw D--B dashed withdots;

trace codeperp(S,H,A,6);
trace codeperp(S,H,B,6);

label.lft(btex $A$ etex,A);
label.bot(btex $B$ etex,B);
label.rt(btex $C$ etex,C);
label.urt(btex $D$ etex,D);
label.top(btex $S$ etex,S);
label.bot(btex $H$ etex,H);


pair AA,BB,CC,DD,HH;
numeric cr;
cr:=0.4;     %coefficient de réduction

AA:=cr[S,A];
BB:=cr[S,B];
CC:=cr[S,C];
DD:=cr[S,D];
HH:=cr[S,H];

draw AA--BB--CC;

---

Le cône de révolution

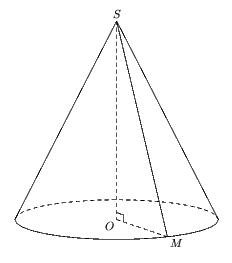
Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,O,S,M;

numeric rb,h;
rb:=3;     % rayon de base
h:=6;      % hauteur

A=(-rb*u,0);
O=(0,0);
B=(rb*u,0);
S=(0,h*u);

path cc;
cc= cercles(O,rb*u);
cc := cc yscaled 0.2;
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

draw A--S--B;

draw S--O dashed evenly;

numeric ang;

ang:=300;  % angle servant à placer M

M:=point (length cc *ang/360) of cc;

draw O--M dashed evenly;
draw S--M;

trace codeperp(S,O,M,6);

label.top(btex $S$ etex,S);
label.llft(btex $O$ etex,O);
label.lrt(btex $M$ etex,M);

fin;

---

Le cône de révolution et sa réduction

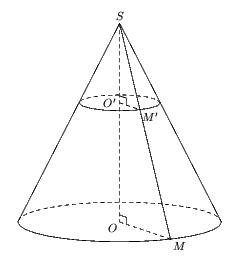
Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,O,S,M;

numeric rb,h;
rb:=3;     % rayon de base
h:=6;      % hauteur

A=(-rb*u,0);
O=(0,0);
B=(rb*u,0);
S=(0,h*u);

path cc;
cc= cercles(O,rb*u);
cc := cc yscaled 0.2;
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

draw A--S--B;

draw S--O dashed evenly;

numeric ang;

ang:=300;  % angle servant à placer M

M:=point (length cc *ang/360) of cc;

draw O--M dashed evenly;
draw S--M;

trace codeperp(S,O,M,6);

label.top(btex $S$ etex,S);
label.llft(btex $O$ etex,O);
label.lrt(btex $M$ etex,M);

pair OO,MM;
numeric cr;
cr:=0.4;

cc:= cercles(O,cr*rb*u);
cc:= cc yscaled 0.2;
cc:=cc shifted cr[S,O];
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

MM:=cr[S,M];
OO:=cr[S,O];

label.lft(btex $O'$ etex,OO);
label.lrt(btex $M'$ etex,MM);

draw OO--MM dashed evenly;

trace codeperp(S,OO,MM,6);

---

La boule ou la sphère

Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,O,S,M;

numeric rb;
rb:=3;   % rayon

A=(-rb*u,0);
O=(0,0);
B=(rb*u,0);


path cc;
cc= cercles(O,rb*u);
draw cc;

cc := cc yscaled 0.2;
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

numeric ang;
ang :=300;   % angle fixant M

M=point (length cc *ang/360) of cc;
draw O--M;

nomme.lft(O);
nomme.lrt(M);

label.urt(btex $R$ etex,0.5[O,M]);

marque_p := "croix";
MarquePoint(O);
marque_p := "rien";


fin;

---

Section par un plan de la boule ou de la sphère

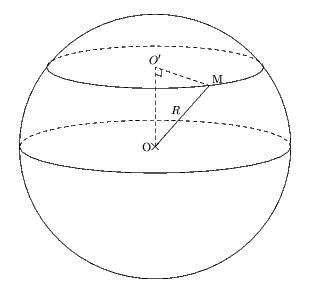
Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,O,S,M,OO;

numeric rb;
rb:=4;   %rayon de la boule

A=(-rb*u,0);
O=(0,0);
B=(rb*u,0);

numeric cr,rr;
cr:=0.6;    %coefficient servant à placer O'
rr:=rb*sqrt(1-cr*cr);

OO=(0,cr*rb*u);

path cc;
cc= cercles(O,rb*u);
draw cc;

cc := cc yscaled 0.2;
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

cc := cercles(O,rr*u);
cc := cc yscaled 0.2;
cc := cc shifted (0,cr*rb*u);
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

numeric ang;
ang :=300;   % angle fixant M

M=point (length cc *ang/360) of cc;

nomme.lft(O);
nomme.urt(M);

draw O--M;

draw O--OO--M dashed evenly;

trace codeperp(O,OO,M,6);

label.top(btex $O'$ etex, OO);
label.ulft(btex $R$ etex, 0.5[O,M]);

marque_p := "croix";
MarquePoint(O);
marque_p := "rien";

---

Cylindre couché

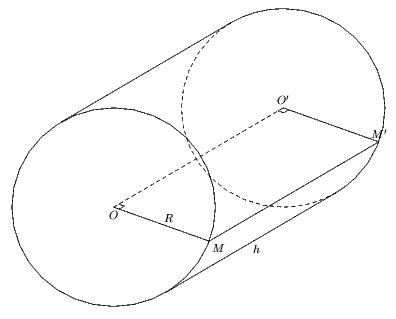
Voici son code:

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,O,AA,BB,OO,M,MM,I;

numeric rb;
rb:=3;     % rayon de base
pair V;
V:=(5u,3u);      % vecteur

O=(0,0);
OO:= O shifted V;

path cc;
cc= cercles(O,rb*u);
draw cc;

path d;
d:=demidroite(O,OO);
I := d intersectionpoint cc;
A:= rotation(I,O,270);
AA:= A shifted V;

B= symetrie(A,O);
BB:= B shifted V;

trace arccercle(BB,AA,OO) dashed evenly;
trace arccercle(AA,BB,OO);

draw A--AA;
draw B--BB;
draw O--OO dashed evenly;

numeric ang;

ang:=340;  % angle servant à placer M

M:=point (length cc *ang/360) of cc;

draw O--M;
trace codeperp(M,O,OO,5);

MM:= M shifted V;
draw OO--MM;
draw M--MM;
trace codeperp(O,OO,MM,5);

label.b

---

Cylindre debout

Voici son code :

u:=1cm;
figure (-8u,-8u,10u,8u);
pair A,B,O,AA,BB,OO,M,MM;

numeric rb,h;
rb:=3;     % rayon de base
h:=6;      % hauteur

O=(0,0);
OO:= O shifted (0,h*u);
A=(-rb*u,0);
AA:= A shifted (0,h*u);
B=(rb*u,0);
BB:= B shifted (0,h*u);

path cc;
cc= cercles(O,rb*u);
cc := cc yscaled 0.2;
draw subpath (0, length cc /2) of cc dashed evenly;
draw subpath (length cc /2,length cc) of cc;

draw cc shifted (0,h*u);

draw A--AA;
draw B--BB;
draw O--OO dashed evenly;

numeric ang;

ang:=300;  % angle servant à placer M

M:=point (length cc *ang/360) of cc;

draw O--M dashed evenly;
trace codeperp(M,O,OO,5);

MM:= M shifted(0,h*u);
draw OO--MM;
draw M--MM;
trace codeperp(O,OO,MM,5);


label.bot(btex $O$ etex,O);
label.top(btex $O'$ etex,OO);
label.lrt(btex $M$ etex,M);
label.top(btex $M'$ etex,MM);

label.urt(btex $R$ etex,0.5[O,M]);
label.rt(btex $h$ etex,0.5[B,BB]);


fin;