Enoncé
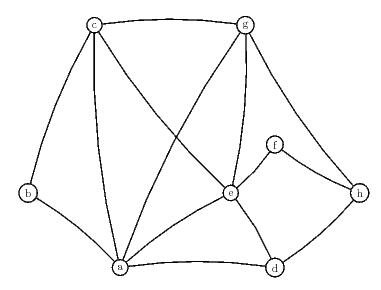
1) Donner la matrice $M$ associé au graphe ci-dessus.
2) Calculer $M^3$.
3) En déduire le nombre de chemin de longueur 3 permettant d’aller de $B$ à $F$.
Résolution à l’aide de Xcas
1) Donner la matrice $M$ associé au graphe ci-dessus.
M:=[[0,1,1,1,1,0,1,0],[1,0,1,0,0,0,0,0],[1,1,0,0,1,0,1,0],[1,0,0,0,1,0,0,1],[1,0,1,1,0,1,1,0],[0,0,0,0,
1,0,0,1],[1,0,1,0,1,0,0,1],[0,0,0,1,0,1,1,0]]
$$ \beginpmatrix 0&1&1&1&1&0&1&0\\ 1&0&1&0&0&0&0&0\\ 1&1&0&0&1&0&1&0\\ 1 &0&0&0&1&0&0&1\\ 1&0&1&1&0&1&1&0\\ 0&0&0&0&1&0&0&1\\ 1&0&1&0&1&0&0 &1\\ 0&0&0&1&0&1&1&0\\ \endpmatrix$$
2) Calculer $M^3$.
P:=M^3
$$ \beginpmatrix 10&8&11&10&12&5&13&4\\ 8&2&7&3&5&2&4&3\\ 11&7&8&6&12&3&10 &5\\ 10&3&6&2&11&1&4&8\\ 12&5&12&11&8&8&13&3\\ 5&2&3&1&8&0&2&6 \\ 13&4&10&4&13&2&6&9\\ 4&3&5&8&3&6&9&0\\ \endpmatrix$$
3) En déduire le nombre de chemin de longueur 3 permettant d’aller de $B$ à $F$.
P[0,5]
$$2$$