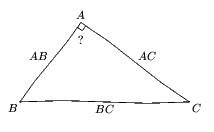
Pour le théorème de Pythagore

Voici son code :
u:=1cm; figuremainlevee(-8u,-8u,10u,8u); pair A,B,C; numeric AB,AC,BC; AB:=4; %choisir les longueurs AC:=3; A:=(0,0); B:=(AB*u,0); C:=(0,AC*u); trace polygone(A,B,C); label.llft(btex $A$ etex,A); %changer les noms des points de la zone de texte label.lrt(btex $B$ etex,B); label.top(btex $C$ etex,C); trace codeperp(B,A,C,5); label.bot(btex $AB$ etex,0.5[A,B]); %changer les longueurs label.lft(btex $AC$ etex,0.5[A,C]); label.urt(btex ? etex,0.5[B,C]); finmainlevee;
Pour la réciproque du théorème de Pythagore
Voici son code :
u:=1cm; figuremainlevee (-8u,-8u,10u,8u); pair A,B,C; numeric AB,AC,BC; BC:=5; %choisir les longueurs AB:=3; AC:=4; B:=(0,0); C:=(BC*u,0); path cc,cb; cc:=arccercle((xpart(C) +AC*u,ypart(C)),(xpart(C)-AC*u,ypart(C)),C); cb:=arccercle((xpart(B)+AB*u,ypart(B)),(xpart(B)-AB*u,ypart(B)),B); A= cc intersectionpoint cb; trace polygone(A,B,C); label.llft(btex $B$ etex,B); %changer les noms des points de la zone de texte label.lrt(btex $C$ etex,C); label.top(btex $A$ etex,A); trace codeperp(B,A,C,5); label.bot(btex ? etex,A shifted (0,-0.3u)); label.bot(btex $BC$ etex,0.5[B,C]); %changer les longueurs label.ulft(btex $AB$ etex,0.5[A,B]); label.urt(btex $AC$ etex,0.5[A,C]); finmainlevee;
Pour le théorème de Thalès dans un triangle
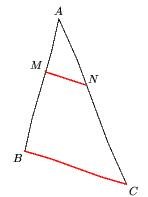
Voici son code :
u:=1cm; figuremainlevee(-8u,-8u,10u,8u); pair A,B,C,M,N; B:=(0,0); A:=(u,4u); C:=(3u,-u); numeric cr; cr:=0.4; M:=cr[A,B]; N:=cr[A,C]; trace segment (B,A); trace segment (A,C); trace segment(M,N) withcolor red withpen pencircle scaled 1.5pt; trace segment(B,C) withcolor red withpen pencircle scaled 1.5pt; label.top(btex $A$ etex,A); %changer les noms des points de la zone de texte label.llft(btex $B$ etex,B); label.lrt(btex $C$ etex,C); label.ulft(btex $M$ etex,M); label.urt(btex $N$ etex,N); finmainlevee;
Pour le théorème de Thalès dans la figure papillon

Voici son code :
u:=1cm; figuremainlevee(-8u,-8u,10u,8u); pair A,B,C,M,N; B:=(0,0); A:=(u,3u); C:=(3u,-u); numeric cr; cr:=-0.4; M:=cr[A,B]; N:=cr[A,C]; trace segment (B,A); trace segment (A,C); trace segment (M,A); trace segment (A,N); trace segment(M,N) withcolor red withpen pencircle scaled 1.5pt; trace segment(B,C) withcolor red withpen pencircle scaled 1.5pt; label.lft(btex $A$ etex,A); %changer les noms des points de la zone de texte label.llft(btex $B$ etex,B); label.lrt(btex $C$ etex,C); label.urt(btex $M$ etex,M); label.ulft(btex $N$ etex,N); finmainlevee;
Triangle rectangle et cercle circonscrit
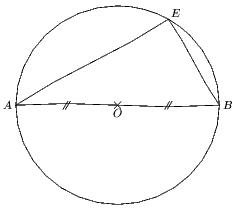
Voici son code :
u:=1cm; figuremainlevee (-8u,-8u,10u,8u); pair A,B,O,E; A:=(-3u,0); O:=(0,0); B:=symetrie(A,O); E:=rotation(B,O,60); trace triangle(A,B,E); trace arccercle(B,E,O); trace arccercle(E,A,O); trace arccercle(A,B,O); trace codesegments(A,O,O,B,2); %trace codeperp(A,E,B,5); label.lft(btex $A$ etex,A); label.rt(btex $B$ etex,B); label.bot(btex $O$ etex,O); label.urt(btex $E$ etex,E); marque_p:="croix"; pointe(O); marque_p:="rien"; finmainlevee;
Deux angles inscrits

Voici son code :
u:=1cm;
figuremainlevee (-8u,-8u,10u,8u);
pair D,A,B,O,E,F;
numeric r;
r:=3;
O:=(0,0);
D:=(r*u,0); %Point à droite du cercle.
A:=rotation(D,O,104);
B:=rotation(D,O,30);
E:=rotation(D,O,200);
F:=rotation(D,O,300);
trace chemin(A,E,B);
trace chemin(A,F,B);
%trace codeangle.urt(B,E,A,1,btex $52^{\circ}$ etex);
trace marqueangle(B,E,A,1);
trace marqueangle(B,F,A,1);
label.ulft(btex $A$ etex,A);
label.urt(btex $B$ etex,B);
label.llft(btex $E$ etex,E);
label.bot(btex $F$ etex,F);
trace arccercle(B,A,O) withcolor red withpen pencircle scaled 1.5pt;
trace arccercle(A,E,O);
trace arccercle(E,F,O);
trace arccercle(F,B,O);
finmainlevee;
Un angle inscrit et un angle au centre

Voici son code :
u:=1cm;
figuremainlevee (-8u,-8u,10u,8u);
pair D,A,B,O,E;
numeric r;
r:=3;
O:=(0,0);
D:=(r*u,0); %Point à droite du cercle.
A:=rotation(D,O,104);
B:=rotation(D,O,30);
E:=rotation(D,O,250);
trace chemin(A,E,B);
trace chemin(A,O,B);
%trace codeangle.urt(B,E,A,1,btex $52^{\circ}$ etex);
trace marqueangle(B,E,A,1);
trace marqueangle(B,O,A,2);
label.ulft(btex $A$ etex,A);
label.urt(btex $B$ etex,B);
label.llft(btex $E$ etex,E);
label.bot(btex $O$ etex,O);
trace arccercle(B,A,O) withcolor red withpen pencircle scaled 1.5pt;
trace arccercle(A,E,O);
trace arccercle(E,B,O);
finmainlevee;