pro-mat.sty facilite l’écriture de documents contenant du calcul matriciel : produit, inverse, déterminant, etc.
Dans le préambule
On rajoute ceci :
\usepackage[xcas]{pro-mat}
matmat
Permet d’afficher une matrice avec la syntaxe XCAS :
\begin{matmat}
matmat([[112,2,cos(alpha)],[sqrt(2),0,1],[1/2,2,3]])
\end{matmat}
On obtient :

promat
Permet d’effectuer des produits de matrices de tailles quelconques. On entre les deux matrices puis des options dans une troisième liste. La première contient la liste des noms des matrices à afficher. Elle peut être vide. On peut mettre en deuxième option trigo si on veut réécrire plus joliment certaines expressions trigonométriques :
Un produit de matrices de tailles différentes :
\begin{promat}
promat([[112,2,0],[0,0,1],[1,2,3]],[[1],[5],[0]],[["R","Z"]])
\end{promat}
On obtient :

Un carré de matrice carré avec l’option trigo…
\begin{promat}
promat([[cos(theta),-sin(theta),0],[sin(theta),cos(theta),0],[0,0,1]],
[[cos(theta),-sin(theta),0],[sin(theta),cos(theta),0],[0,0,1]],
[["R","R","R^2"],trigo])
\end{promat}
On obtient :

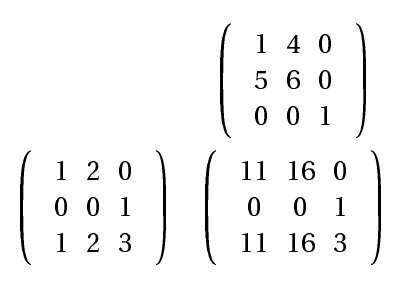
Un produit de matrices de même taille sans option :
\begin{promat}
promat([[1,2,0],[0,0,1],[1,2,3]],[[1,4,0],[5,6,0],[0,0,1]],[[]])
\end{promat}
On obtient :
detmat
Permet de calculer des déterminants. On entre la matrice et en option on peut rajouter factor si on veut le résultat factorisé.
Un calcul de déterminant sans factorisation~:
\begin{detmat}
detmat([[cos(theta),-sin(theta),0],[sin(theta),cos(theta),0],[0,0,1]],[])
\end{detmat}
On obtient :

Un calcul de déterminant factorisé~:
\begin{detmat}
detmat([[1-t,2,0],[1,2-t,0],[0,0,1-t]],[factor])
\end{detmat}
On obtient :

invmat
Permet de calculer l’inverse d’une matrice…inversible. On entre la matrice.
\begin{invmat}
invmat([[a,-b,3],[1,0,0],[0,0,1]])
\end{invmat}
On obtient :

puimat
Permet de calculer les puissances d’une matrice. On entre la matrice, la puissance et la liste des options : trigo ou rien.
Sans trigo
\begin{puimat}
puimat([[1,1,1],[1,1,1],[1,1,1]],5,[])
\end{puimat}
On obtient :

Avec trigo
\begin{puimat}
puimat([[cos(theta),-sin(theta),0],[sin(theta),cos(theta),0],[0,0,1]],
3,[trigo])
\end{puimat}
On obtient :
