Géométrie analytique au collège avec Xcas

Enoncé

Dans un repère orthonormé $(O,I,J)$, on donne les points suivants :
$$A(1~;~2) \qquad B(-2\sqrt3~;~\sqrt3) \qquad C(-1~;~-2)$$

1) Faire une figure.

2) Montrer que $ABC$ est un triangle équilatéral.

Résolution à l’aide de Xcas

1) Faire une figure.

Dans une session Xcas, on ajoute une fenêtre de géométrie 2D :

Menu Editer —> Ajouter –> geo2d exact

On crée ensuite les points et le triangle en plaçant les commandes à gauche de la fenêtre graphique.


A:=point(1,2) ;
B:=point(-2*sqrt(3),sqrt(3)) ;
C:=point(-1,-2) ;
triangle(A,B,C) ;


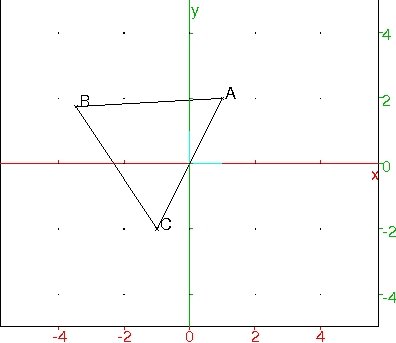
2) Montrer que $ABC$ est un triangle équilatéral.

On calcule successivement les longueurs en plaçant les instructions en dessous de la fenêtre graphique :


normal(longueur(A,B))


$$2~\sqrt5$$


normal(longueur(A,C))


$$2~\sqrt5$$


normal(longueur(B,C))


$$2~\sqrt5$$